DOMINIO Y RANGO DE UNA FUNCION

El dominio de una función f ( x ) es el conjunto de todos los valores para los cuales la función está definida, y el rango de la función es el conjunto de todos los valores que f toma.

Ejemplo 1:

Considere la función mostrada en el diagrama.

Aquí, el dominio es el conjunto { A , B , C , E }. D no está en el dominio, ya que la función no está definida para D .

El rango es el conjunto {1, 3, 4}. 2 no está en el rango, ya que no hay letra en el dominio que se enlace con el 2.

Ejemplo 2:

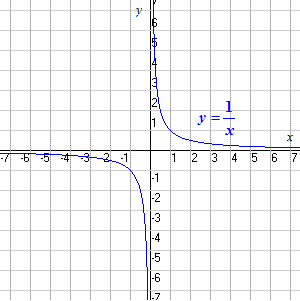
El dominio de la función

f ( x ) = 1/ x

es todos los números reales excepto el cero (ya que en x = 0, la función no está definida: la división entre cero no está permitida!).

El rango también es todos los números reales excepto el cero. Puede ver que hay algún punto en la curva para cada valor de y excepto para y= 0.

Los dominios pueden también estar explícitamente especificados, si hay valores para los cuales la función pudiera estar definida, pero que no deseamos considerarlos por alguna razón.

Ejemplo 3:

La notación siguiente muestra que el dominio de la función está restringido al intervalo (–1, 1).

f ( x ) = x 2 ,     –1  x  1

La gráfica de esta función es como se muestra. Dese cuenta de los círculos abiertos, que muestran que la función no está definida en x = –1 yx = 1. Los valores del rango de y desde 0 hasta el 1 (incluyendo el 0, pero no incluyendo el 1). Así el rango de la función es

0  y < 1.